Cijfers weergeven in een vliegtuig (definitie)

2024 Auteur: Leah Sherlock | [email protected]. Laatst gewijzigd: 2023-12-17 05:45

Het vermogen om verschillende vormen correct weer te geven op het vlak van het vel, canvas en elk ander oppervlak is een behoorlijk belangrijke vaardigheid. En bovenal is het zowel belangrijk voor mensen van de kunst: schilders, beeldhouwers, grafici, ontwerpers (van binnenruimtes en de architecturale omgeving), als voor mensen van de wetenschap: wiskundigen, natuurkundigen, ontwerpers, uitvinders.

Maar het is ook belangrijk voor een persoon die ver van deze sferen is om te leren hoe hij de wereld om hem heen correct kan waarnemen en weergeven. Dit helpt om al zijn veelzijdigheid veel beter te begrijpen. Als u niet voldoende idee heeft hoe u dit correct moet doen, dan zult u hoogstwaarschijnlijk niet slagen in een project, afbeelding of tekening van een uitvinding. Dat wil zeggen, deze vaardigheid is zowel belangrijk voor het oplossen van eenvoudige, alledaagse taken als voor taken die een globale, universele betekenis hebben.

Een beetje geschiedenis

Sinds de oudheid hebben mensen geprobeerd weer te geven wat ze om zich heen zagen: andere mensen, enkele primitieve gebouwen uit die tijd, een verbazingwekkend mooie wereld van planten en dieren, majestueuze bergen en gewoon dingen, huishoudelijke artikelen. Dat wil zeggen, de wereld in al zijn diversiteit en grootsheid.

Maar toen hadden ze nog geen idee hoe het nauwkeurig en vakkundig kon worden gedaan, zodat de weergave van verschillende driedimensionale objecten op een vliegtuig echt realistisch, levend was. De persoon beschikte niet over de relevante kennis en bovendien waren er geen speciale vaardigheden, behalve misschien de meest elementaire.

In eerdere bronnen wordt gezegd dat het eerste schilderij ter wereld uit slechts één lijn bestond die langs de schaduw van een persoon liep die door de zon op de muur werd geworpen. Dat wil zeggen, de natuur zelf suggereerde in welke richting het de moeite waard was om op zoek te gaan naar de juiste oplossing voor dit probleem.

En deze vraag baarde de man van die tijd ook zorgen om deze reden: hij wilde niet alleen het volumineuze levende silhouet bewonderen, het origineel, om zo te zeggen, maar probeerde een ruimtelijk object op een vliegtuig vast te leggen. En hij deed dit zodat hij op deze manier ofwel zijn huis of een voor hem heilige plaats kon versieren, of een bundel met een foto mee kon nemen en deze naar elke afstand kon verplaatsen.

Patroon geometrie

En wat je ook zegt, maar jaren gingen voorbij, eeuwen gingen voorbij, en op de een of andere manier, naarmate de beschaving zich ontwikkelde, leerden mensen geleidelijk complexe figuren weer te geven in een tweedimensionale ruimte, dat wil zeggen in een vliegtuig. Pas nu begon de nauwkeurigheid van de afmetingen en verhoudingen van de afgebeelde objecten erg bij benadering te lijken.

Maar de vraag hoe correct de weergave van de figuur in het vliegtuig en in hoeverre ze overeenkomen met het volume van de originele objecten, werd ooit zeer relevant. Op de een of andere manier heet een nieuwe wetenschapgeometrie. Om precies te zijn, de sectie ervan is beschrijvende geometrie.

Hier bestudeert ze gewoon vormen en vlakken, lijnen en punten, evenals hun relatie tot elkaar - zowel in de driedimensionale als in de tweedimensionale ruimte.

Conversiemethoden

Een belangrijk kenmerk in de beeldende kunst is de weergave van figuren op het beeldvlak. Dit is tenslotte het vastleggen van driedimensionale ruimtelijke objecten in tweedimensionaliteit. Namelijk: het complex moet worden omgezet in een eenvoudig, dat wil zeggen, een object met een lengte, breedte, hoogte moet worden overgebracht naar een vlak.

En beschrijvende geometrie maakt zulke "overgangen" dankzij enkele methoden. Het zijn er in totaal zo'n zes. Dit zijn de drie belangrijkste en de meest populaire over de hele wereld:

• perspectief (wanneer het afgebeelde object in de ruimte wordt verwijderd);
• orthogonale projectie (parallel projectie, waarbij de stralen loodrecht op het vlak staan);
• schuine projectie (parallel projectie, waarbij de stralen gekanteld zijn ten opzichte van het vlak).

Het afgebeelde object verschijnt vrij duidelijk in axonometrische projectie (inclusief orthogonaal en schuin). Maar het wordt het duidelijkst en echt geprojecteerd wanneer het in perspectief wordt getoond. En het zijn de bovenstaande methoden die grotendeels de vraag oplossen hoe figuren in een vliegtuig moeten worden weergegeven.

Perspectief

Perspectief neemt de meest eervolle plaats in onder andere beeldmethoden. Omdat het menselijk oognet als een cameralens ziet het de omringende ruimte op een vergelijkbare manier. Dingen die verder van de waarnemer verwijderd zijn, lijken kleiner en soms veel kleiner dan wanneer ze dichtbij zijn.

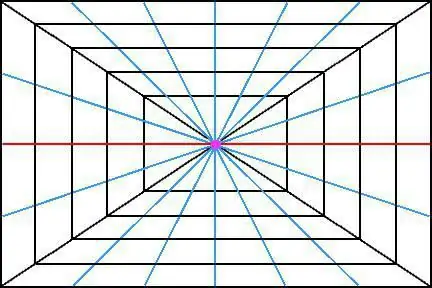
Neem bijvoorbeeld de afbeelding van een kubus in de ruimte. Als in feite alle randen evenwijdig aan elkaar zijn, kan het lijken alsof de randen op één punt samenkomen (of zouden moeten convergeren) als je naar dit object in de verte kijkt. En, wat het meest interessant is, ze zouden niet slechts op één punt moeten samenkomen, maar één enkel snijpunt moeten hebben.

Dankzij de meesters van de Renaissance: Albrecht Dürer, Piero Della Francesca, Andrea Mantegna, Leon Batista Alberti, weet de moderne schilderkunst wat direct lineair perspectief is, hoe de hoogte van de horizon en verdwijnpunten te bepalen.

En het wereldberoemde genie - Leonardo da Vinci - voerde voor het eerst het concept van luchtperspectief aan. Dit omvat een verandering in de kleur, toon van het object, veranderingen in de contrastkenmerken (afnemend naarmate het object verder weg beweegt).

Orthografische projectie

Orthogonaal wordt parallelle projectie genoemd, die is gericht op een rechte lijn, die loodrecht op het vlak staat. Tijdens het aanbrengen blijven de afmetingen van de contouren van het object ongewijzigd. Dat wil zeggen, het object wordt weergegeven zonder vervorming.

Het geprojecteerde driedimensionale object wordt als het ware ontleed in drie aanzichten: van opzij, van voren en van bovenaf. En als je dit allemaal tegelijkertijd bekijkt, kun je toevoegeneen weergave van hoe een object er in volume uitziet. Tegelijkertijd blijven de afmetingen van de figuur ongewijzigd, zowel in het driedimensionale beeld als in het tweedimensionale.

Schuine projectie

Deze projectie is onderverdeeld in nog een aantal ondersoorten, namelijk:

• isometrische weergave;
• dimetrische projectie;
• trimetrische projectie.

Isometric heeft vervormingscoëfficiënten in alle 3 assen (lengte, breedte, hoogte). Dat wil zeggen, de hoeken tussen paarsgewijs genomen assen zijn gelijk aan 120 graden. In de dimetrische zijn de vervormingen langs de 2 assen gelijk, en de derde is anders. En in de trimetrische projectie zijn alle vervormingscoëfficiënten (dat wil zeggen langs alle 3 assen) verschillend.

Vormen van rotatie

Als een rechthoekige driehoek roteert langs de as van een van de twee benen, zal de derde zijde (hypotenusa) een nieuwe figuur beschrijven die een kegel wordt genoemd. En als je een rechthoek (vierkant) langs een van zijn zijden draait, krijg je een cilinder. Als de halve cirkel draait, komt er een bol uit.

Hieruit volgt dat door het vlak langs een as te roteren, we de zogenaamde rotatiecijfers krijgen.

Deze figuren hebben een rotatie-as. Hoe ze er in het vliegtuig uitzien, hangt af van hun plaatsing ten opzichte van ooghoogte. De boven- en onderkant van een cilinder zijn bijvoorbeeld in wezen cirkels. En als je ze in een vliegtuig bekijkt, zien ze eruit als ellipsen.

Maar de taak wordt nog moeilijker als, bij het weergeven vanruimtelijke figuren op het vlak, ze hebben een schuine as. Het is belangrijk dat de contouren van de omwentelingslichamen op gelijke afstand van de as van de laatstgenoemde liggen.

Een beetje over clair-obscur

Clair-obscur speelt een belangrijke rol bij het weergeven van figuren in een vliegtuig. Omdat het volume van het afgebeelde object niet alleen wordt gecreëerd door lijnen, maar ook door de juiste verdeling van licht en schaduw aan de zijkanten. En dan ziet het er behoorlijk volumineus uit in het vlak van een tweedimensionaal oppervlak.

Zo is het weergeven van figuren in het vliegtuig, het bepalen van hun afmetingen, de kenmerken van de juiste overlay van lichtheid en donkere vlekken heel goed mogelijk dankzij de bovenstaande methoden. En, belangrijker nog, dit zijn echt bewezen methoden in de praktijk, die worden gebruikt door toonaangevende experts van deze tijd.